量子開放系のダイナミクス
近年、ナノテクノロジーなど、微小世界に対する実験技術が発展し量子力学的原理を用いた新たな技術創成が進んでいます。例えば、量子情報処理や量子輸送等の分野では、電子や原子核、イオン、光子といったミクロな実体に対する精密な制御が可能となってきています。しかし、ミクロな実体を完全に孤立させることはできません。これらは周囲をとりまく環境世界の影響を必ず受けています。
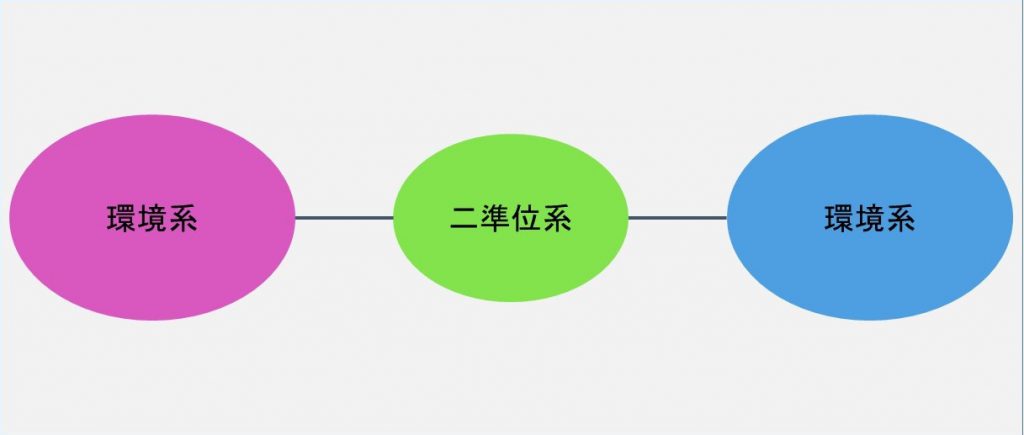
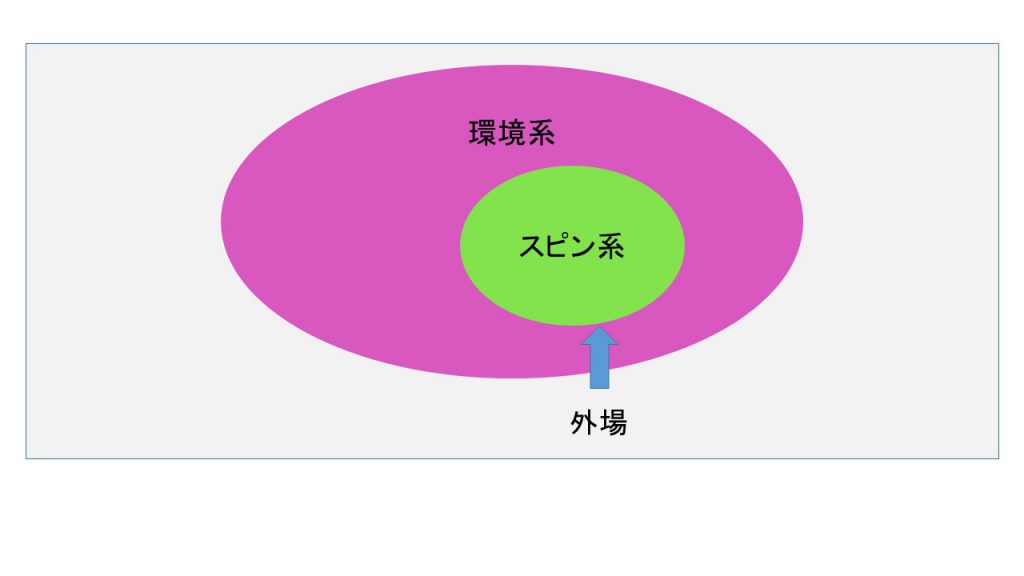
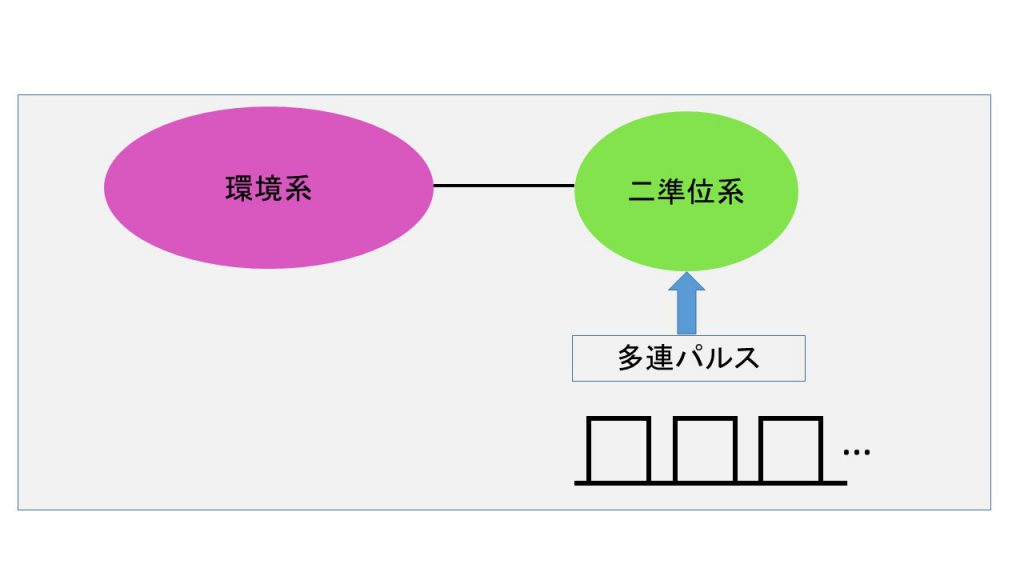
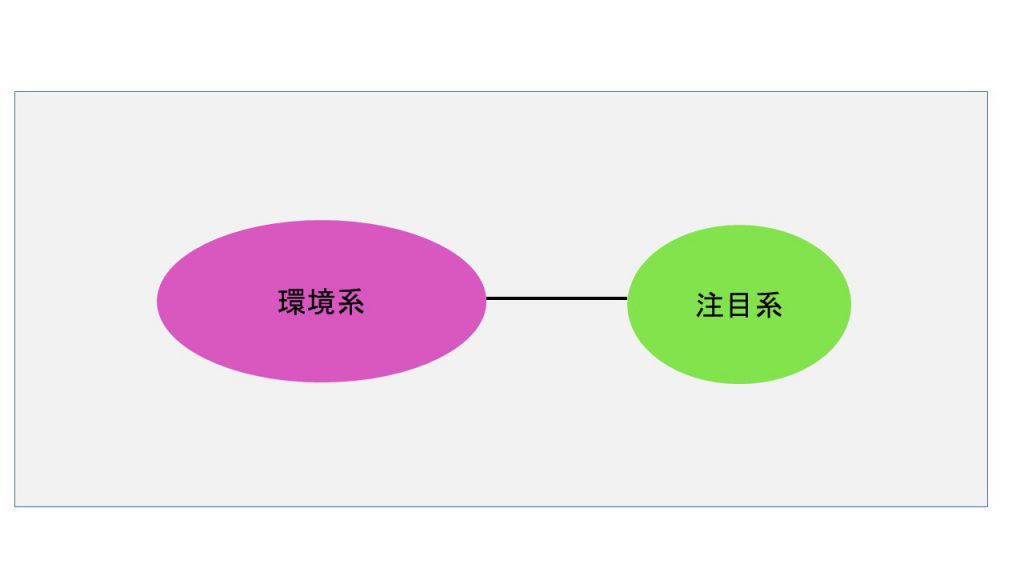
そこで、上記の技術創成には、この環境世界の影響の評価が必須です。多くの場合、環境世界の影響は量子制御を困難にします。しかし、最近は環境世界の影響を利用した制御についての提案も行われており、今後の理論発展が期待されています。この環境世界を取り込んだモデルを量子開放系と呼びます。当研究室では、量子情報処理や量子輸送等に対する環境世界の影響を評価するとともに、この利用方法の提案に取り組んでいます。
研究内容
エネルギー問題の深刻な現在、エネルギー消費量の見直しが行われています。特に、データセンターにおける大規模コンピュータのCPUからの排熱量の増加が懸念されています。なぜなら、排熱量増加は、熱暴走を防ぐための冷却に必要なエネルギーの増加を意味するからです。そのため、CPUを構成する半導体における熱設計の重要性が増しています。例えば、半導体が発生した熱自体を演算に利用するなど、ミクロレベルでの熱制御の提案が行われ始めています。当研究室では、このような研究動向をふまえ、ミクロレベルでの熱機関設計を行っています。
熱量子ポンピング
「熱エネルギーは、熱いものから冷たいものへ流れる」というのが我々の常識です。ミクロレベルでも、この常識を考慮しなければならないのか？それとも、常識ににとらわれずに熱機関を設計できるのか？この問いに答えるべく、２準位系が２種類の熱浴と相互作用する、左図のような系に対する定式化を行っています。この研究は、科学研究費 基盤(B) の一環として行い、論文 ”Nonadiabatic effect on the quantum heat flux control” Phys. Rev. E 89, 052108 として発表されています。また、2016年開始した科学研究費 基盤(C)の研究成果として論文”Energy backflow and non-Markovian dynamics” Phys. Rev. A 93, 012118を発表しています
量子開放系のダイナミクスを論ずる際、従来は注目系と環境系が初期時刻において相関を持たない、という仮定を置くことが多く行われてきました。しかし、この仮定はミューオン緩和現象を除き、実際の実験状況とかけ離れている場合が多いと考えられます。特に初期相関が影響を及ぼすと思われる線形応答についての研究を行いました。
線形応答への初期相関の影響
通常の線形応答理論では、外場の印加と同時に注目系（例えばスピン）と環境系（例えばスピンを含む試料）が相互作用を開始する設定がなされています。しかし、外場印加開始時点では試料全体が熱平衡状態にあり、注目系と環境系の間には量子的な初期相関があると考えるのが自然です。この初期相関が過渡的な線形応答に与える場合については、Phys. Rev. A 82, 044104にて議論しています。また定常的な線形応答に対する初期相関の影響についてはPhys. Rev. E 80, 021128で論じています。
近年、量子力学の原理を用いた情報処理についての研究が活発に行われるようになってきました。量子暗号、量子コンピュータといった言葉の入った見出しの新聞記事を目にされた方も多いと思います。しかし、ビット値を担う量子は周りの環境世界からの影響に脆いことがこれらのスキーム実現に対する大きな障害となっています。当研究室では、この障害を取り除く手法の開発についての研究を行いました。
多連パルス制御
量子情報処理においては、量子力学的重ね合わせ状態が重要な役割を果たします。この重ね合わせ状態の利用により、例えば、現在のコンピュータの行う分岐処理が不要となり、計算を効率化することが可能となります。しかし、重ね合わせ状態が環境世界からの影響に脆弱であることが量子情報処理実現の障害となっています。この研究では、多連パルスを重ね合わせ状態に印加することにより、環境世界の影響による減衰時間を延長できることを示しました。その内容は、Phys. Rev. A 66, 032313にて議論しています。また、環境系に特徴的な振動時間がある場合には、パルス印加時間をその振動周期に合わせることにより、実効的に重ね合わせの度合いの減衰時間を延長できることは、Phys. Rev. A 68, 052302にて論じています。
量子開放系のダイナミクスを記述する際の方法論の一つとして、射影演算子法があります。従来、密度行列の時間発展を記述する、マスター方程式を求めるために用いられてきたこの方法の拡張を行っています。
ハイゼンベルグ表示における射影演算子法
射影演算子法は、量子開放系のダイナミクスを記述するために多用されてきましたが、その利用先は密度行列に対するマスター方程式に限られてきました。本研究では、全系の時間発展演算子に注目することにより、物理量に対するハイゼンベルグ方程式にも適用可能となるように射影演算子法を拡張できることをPhys. Rev. E 60, 2636にて示しました。最近の研究で、この方法は完全計数統計のマスター方程式導出にも適用可能であることがわかりました。